Pythagorean theorem

"I have no difficulty in imagining an anthology of the most beautiful fragments of world poetry in which the Pythagorean theorem would also find its place. Why not? There is that shock that is innate to great poetry, and a form wisely reduced to the most basic terms. indispensable, and a grace that not all poets have been granted ". Wislawa Szymborska

Pythagoras of Samos about 565 - about 500 BC (School of Athens Raphael, bottom left with the open book)

Pythagoras, son of Mnesarco, engraver of precious stones for rings, was born in Samos.

Young and greedy for science, he abandoned his homeland and was initiated into all the mystery rites.

He was in Egypt and learned the language, then he was with the Chaldeans and the Magi, subsequently in Crete and then, by now forty, he returned to Samo, but found his homeland under the tyranny of Polychrates, he sailed towards Crotone of Italy: here he gave laws to the Italiots and achieved great fame together with his followers, who, in number of about three hundred, administered the public affairs, so that their government was almost an aristocracy.

Sosicrates in the Successions of the Philosophers says that Pythagoras, questioned by Leonte, tyrant of Fliunte: "Who are you?", Replied: "Philosopher".

He used to say that life is similar to a panegyry: as in fact some participate in this to fight, others to trade, still others, and they are the best, to assist, so in life, he said, some are born slaves of glory and hunters of gain, other philosophers greedy for the truth.

Some claim that Pythagoras did not leave even a single piece of writing, although he was unable to prove it, while others claim that he wrote three works: On Education, On the State and On Nature.

From these works some general precepts of Pythagoras are handed down.

He forbids us to pray for ourselves because we don't know what is useful for us.

He calls drunkenness, they damage and condemn any excess.

He advises to cultivate the pleasures of love in winter, not in summer; and in autumn and spring that they are lighter.

He distinguishes the life of man: "Childhood twenty years, adolescence twenty, youth twenty, old age twenty".

These periods correspond to the seasons: spring, summer, autumn and winter.

Above all, Pythagoras looked to the arithmetic form of geometry and discovered the monochord canon.

Apollodorus, the theorist of calculus, claims that he sacrificed a massacre of oxen, for having discovered that the square of the hypotenuse in a right triangle is equivalent to the squares of its sides (catheti).

Pythagoras forbade eating animals that have the privilege of the soul in common with us.

All the Pythagorean doctrines were not known until the age of Philolaus, who divulged the three famous works, which Plato had bought for a hundred minas.

No less than six hundred disciples attended his nocturnal audiences, and those who were deemed worthy of seeing him wrote to their families that they had had a great lot.

When he was angry he punished neither slave nor free man.

He forbade eating beans because they corrupt.

Pythagoras died in this way: sitting together with friends in the house of Milone, it happened that his house was set on fire, out of envy, by one who had not been worthy to be welcomed by Pythagoras. Others say that the Crotonese themselves did this, fearing that it wanted to become a tyrant.

Pythagoras found himself abandoned to himself and when he reached a place full of beans, in order not to cross it he stopped, saying that it was preferable to be caught rather than trampled on them: and so he was slaughtered by his pursuers.

Lives of the philosophers, Diogenes Laertius

Everything is number

Pythagoras developed a theory of the "principle of all things" referred to the number, perhaps also observing that the reduction of things to numbers was based on similarities between different realities: the relationships between the strings of different lengths of a lira, between metal mallets of different weight.

The number therefore considered not as an abstract but as a concrete entity.

While other Ionian philosophers identified the first principles of reality in water, air or fire, the Pythagoreans had identified them in the number: the number makes reality intelligible, constituting its profound nature.

The Pythagorean school lasted over one hundred and fifty years and could count on almost three hundred students.

Hippasus was one of the first Pythagoreans, the leader of the "akusmatics", ie the candidates for initiation, while Pythagoras directed the "mathematicians", who had already begun.

The theorem and its proofs

On the Babylonian tablet Plimpton 322, engraved a millennium before the birth of Pythagoras, a scribe had indicated about fifteen groups of three integers for which the rule was that the sum of the square of two of them was equal to the square of the third.

The Babylonians therefore possessed a result, but they had not proved it.

To date there are about 400 proofs of the Theorem, the most classic of which is the one proposed by Euclid, in the first book of the Elements, prop. XLVII.

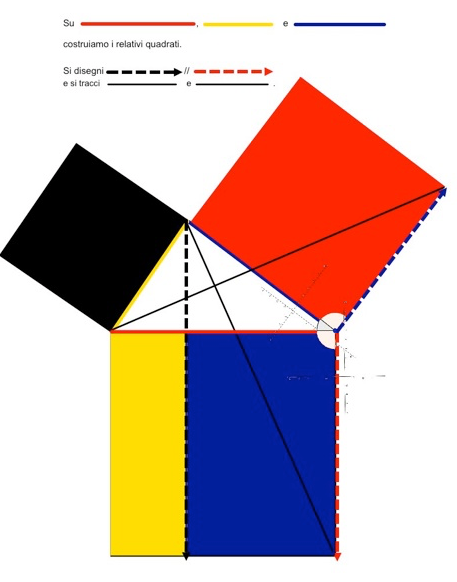
Euclid breaks down the square built on the hypotenuse into two rectangles and demonstrates that the surface area of the small rectangle is equal to the area of the square built on the smaller side, while that of the large rectangle is equal to the area of the square built on the larger side.

Garfield's proof

A geometric proof was found in 1876 by James Abraham Garfield, who later became the twentieth President of the United States.

http://rudimatematici-lescienze.blogautore.espresso.repubblica.it/2009/04/15/il-teorema-di-pitagora/

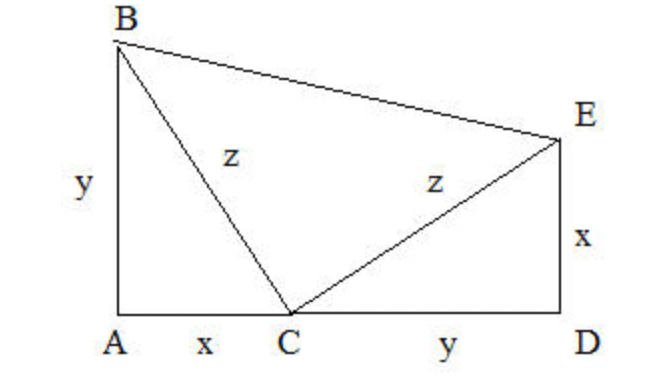
Let ABC be our triangle; on it we construct the triangle CDE (equal to ABC and with CD continuation of AC) and the triangle BCE which results by isosceles construction (by construction, the sides BC and CE are equal).

Basically, we have such a thing as in the picture.

Now, considering that the angle in A is right, we have that it is ACB + ECD = 90 °, as internal angles are not right of equal right-angled triangles; from this, we have that by construction it is BCE = 90 °.

Let us now consider the trapezoid of bases BA and ED. Its area is:

S = (x + y) * (x + y) / 2 = (x + y) ^ 2/2

But this area must be equal to the sum of the areas of the three triangles that form the trapezoid:

S = x * y / 2 + z ^ 2/2 + x * y / 2 = (z ^ 2 + 2xy) / 2

By equating the two areas and multiplying both terms by 2:

(x + y) ^ 2 = z ^ 2 + 2xy

x ^ 2 + y ^ 2 + 2xy = z ^ 2 + 2xy

x ^ 2 + y ^ 2 = z ^ 2

Q.E.D.

Examples of physical proofs of the Theorem exist and are found online.

Incommensurabili

Let us consider an isosceles right triangle with legs of length 1: the theorem confirms that the hypotenuse will measure the square root of 2: the ratio between the diagonal and the side of a square cannot be expressed as an integer.

In other words, there is no submultiple common to both: diagonal and side of the square are immeasurable.

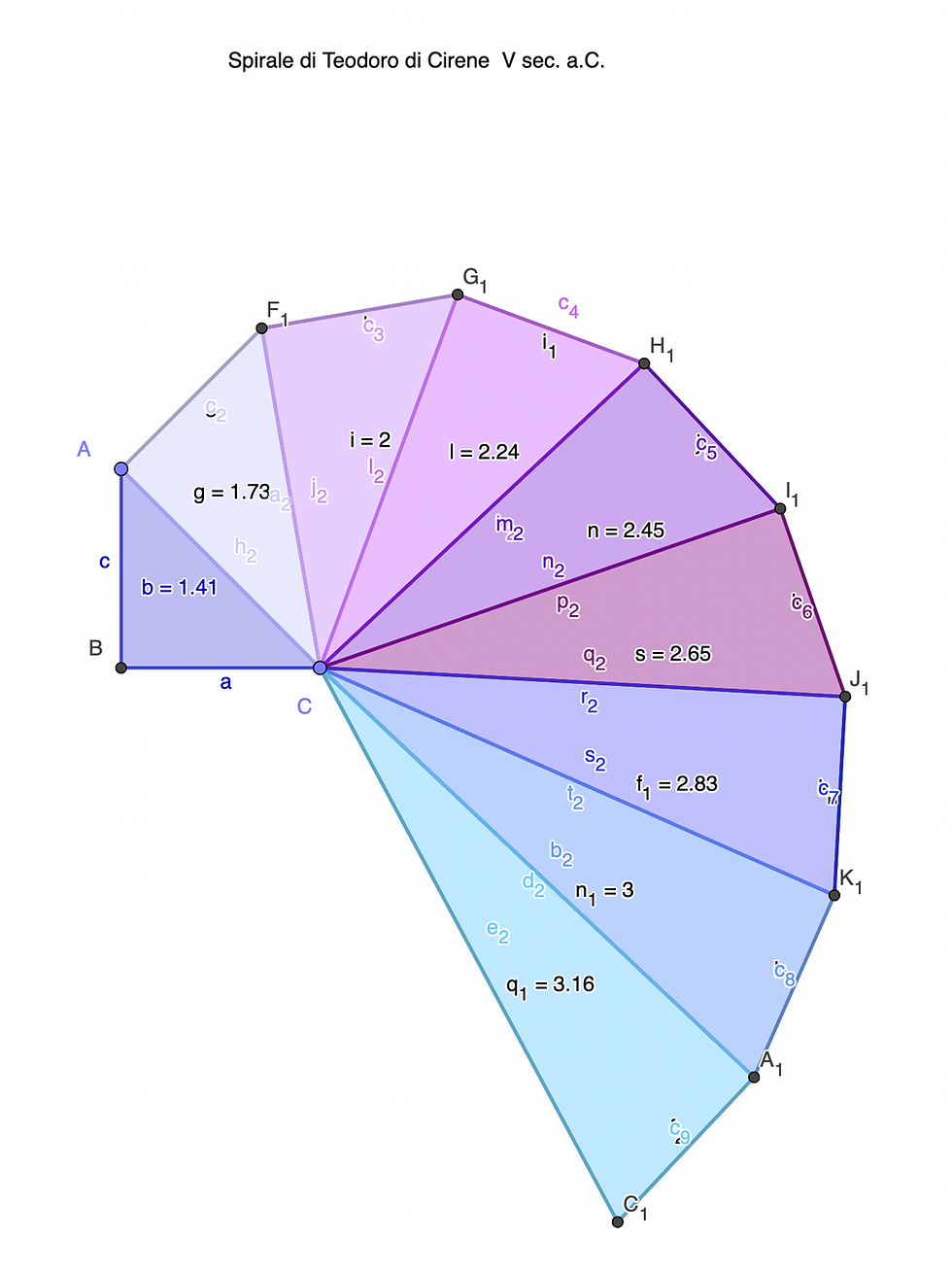
This discovery represented a real tragedy for the Pythagoreans.

For some historians this could have represented the collapse of Pythagorean philosophy.

All this certainly did not cast doubt on the trust in reason among the Pythagoreans, so much so that other authors argue that the Pythagoreans were perfectly capable of conceiving the real number, while continuing to give the term number the meaning of a whole number.

Aristotle states that Plato's doctrine is purely and simply that of the Pythagoreans, to whom he would have changed only one word, writing "ideas" instead of "numbers".

Does the Pythagorean Theorem hold regardless of the regular polygon constructed on the sides of the right triangle?

After having verified the Pythagorean theorem in traditional contexts we can reflect on the possibility that the Theorem can also be verified by constructing other regular polygons, besides the square, on legs and hypotenuse.

The construction of GeoGebra confirms what is reported in the question.

Fermat and the Theorem

The history of mathematics attests to us that the mathematician Pierre de Fermat, who lived in the 1600s, had wondered if there were positive integer solutions of the equation x ^ n + y ^ n = z ^ n when n is greater than 2.

He wrote that he had solved his conjecture but no proof was ever found.

It was the British mathematician André Weils, over 300 years later, in 1994, who proved that there are no positive integer solutions if the exponent is an integer greater than 2.

Is the Pythagorean Theorem always valid? Beyond Euclidean geometry

Bibliography

Lives of the philosophers Diogenes Laertius 2000 Laterza ed.

The art of mathematics Simone Weil, André Weil 2018 Adelphi

The parrot theorem Denis Guedj 2000 Longanesi

History of mathematics Carl B. Boyer 1980 Oscar Mondadori