Il teorema di Pitagora

"Non ho difficoltà a immaginare un'antologia dei più bei frammenti della poesia mondiale in cui trovasse posto anche il teorema di Pitagora. Perchè no? Lì c'è quella folgorazione che è connaturata alla grande poesia, e una forma sapientemente ridotta ai termini più indispensabili, e una grazia che non a tutti i poeti è stata concessa". Wislawa Szymborska

Pitagora di Samo 565 circa - 500 circa a.C. (Scuola di Atene Raffaello, in basso a sx con il libro aperto)

Pitagora, figlio di Mnesarco, incisore di pietre preziose per anelli, nacque a Samo.

Giovane ed avido di scienza, abbandonò la sua patria e fu iniziato a tutti i riti misterici.

Fu in Egitto e ne apprese la lingua, poi fu presso i Caldei ed i Magi, successivamente in Creta e quindi, ormai quarantenne, tornò a Samo, ma trovata la patria sotto la tirannide di Policrate, fece vela verso Crotone d'Italia: qui diede leggi agli Italioti e conseguì grande fama insieme con i suoi seguaci, che in numero di circa trecento amministravano la cosa pubblica, si che il loro governo fu quasi una aristocrazia.

Sosicrate nelle Successioni dei filosofi dice che Pitagora, interrogato da Leonte, tiranno di Fliunte: "Chi sei?", abbia risposto: "Filosofo".

Era solito dire che la vita è simile ad una panegiria: come infatti alcuni partecipano a questa per lottare, altri per commerciare, altri ancora, e sono i migliori, per assistervi, così nella vita, diceva, alcuni nascono schiavi della gloria e cacciatori di guadagno, altri filosofi avidi della verità.

Alcuni affermano che Pitagora non lasciò neppure uno scritto, pur non riuscendo a dimostrarlo, altri invece sostengono che scrisse tre opere: Della Educazione, Dello Stato e Della Natura.

Da queste opere si tramandano alcuni precetti generali di Pitagora.

Ci vieta di pregare per noi stessi perchè non sappiamo cosa ci sia utile.

Chiama l'ubriachezza, danno e condanna ogni eccesso.

Consiglia di coltivare i piaceri d'amore d'inverno, non d'estate; e d'autunno e di primavera che siano più lievi.

Distingue la vita dell'uomo: "Fanciullezza venti anni, adolescenza venti, giovinezza venti, vecchiaia venti".

Questi periodi corrispondono alle stagioni: primavera, estate, autunno e inverno.

Soprattutto Pitagora attese alla forma aritmetica della geometria e scoprì il canone monocordo.

Apollodoro, il teorico del calcolo, afferma che egli sacrificò una ecatombe di buoi, per avere scoperto che il quadrato dell'ipotenusa in un triangolo rettangolo è equivalente ai quadrati dei suoi lati (cateti).

Pitagora proibiva di mangiare gli animali che hanno in comune con noi il privilegio dell'anima.

Tutte le dottrine pitagoriche non furono note fino all'età di Filolao, il quale divulgò le tre celebri opere, che Platone si fece comprare per cento mine.

Non meno di seicento discepoli partecipavano alle sue udienze notturne e quelli che erano ritenuti degni di vederlo, scrivevano ai familiari di avere avuto una grande sorte.

Quando era irato non puniva né schiavo né uomo libero.

Vietava di mangiare le fave perchè corrompono.

Pitagora morì in questo modo: sedendo insieme con amici nella casa di Milone, accadde che la casa di costui fu incendiata, per invidia, da uno che non era stato degno di essere accolto da Pitagora. Altri dicono che gli stessi Crotonesi fecero ciò, temendo che esso volesse diventare tiranno.

Pitagora si trovò abbandonato a sé stesso e giunto in una località piena di fave, per non attraversarla si fermò, dicendo che era preferibile essere preso piuttosto che calpestarle: e così fu sgozzato dagli inseguitori.

Vite dei filosofi, Diogene Laerzio

Tutto è numero

Pitagora elaborò una teoria del "principio di tutte le cose" riferita al numero, forse anche osservando che la riduzione delle cose ai numeri si fondava su somiglianze tra realtà diverse: i rapporti tra le corde di diversa lunghezza di una lira, tra magli di metallo di diverso peso.

Il numero quindi considerato non come entità astratta ma concreta.

Mentre altri filosofi ionici individuavano i principi primi della realtà nell'acqua, nell'aria o nel fuoco, i Pitagorici li avevano individuati nel numero: il numero rende intellegibile la realtà, costituendone la sua natura profonda.

La scuola pitagorica durò oltre centocinquant'anni e potè contare su quasi trecento allievi.

Ippaso fu uno dei primi pitagorici, il capo degli "akusmatici", ossia i candidati all'iniziazione, mentre Pitagora dirigeva i "matematici", che erano già iniziati.

Il teorema e le sue dimostrazioni

Sulla tavoletta babilonese Plimpton 322, incisa un millennio prima della nascita di Pitagora, uno scriba aveva indicato una quindicina di gruppi di tre numeri interi per i quali valeva la regola che la somma del quadrato di due di essi era uguale al quadrato del terzo.

I Babilonesi quindi possedevano un risultato, ma non lo avevano dimostrato.

A tutt'oggi esistono circa 400 dimostrazioni del Teorema, la più classica delle quali è quella proposta da Euclide, nel I libro degli Elementi, prop. XLVII.

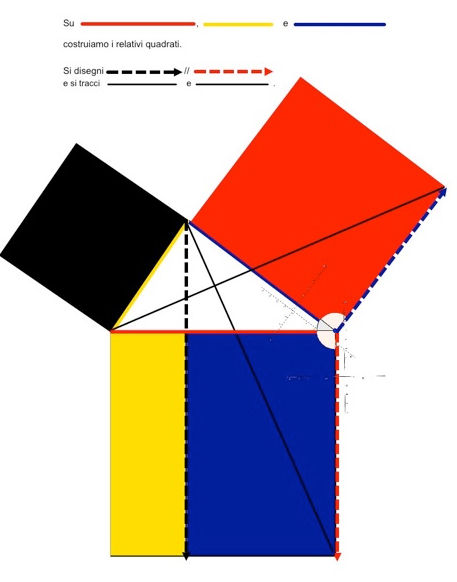
Euclide scompone il quadrato costruito sull'ipotenusa in due rettangoli e dimostra che l'area della superficie del rettangolo piccolo equivale all'area del quadrato costruito sul cateto minore, mentre quella del rettangolo grande equivale all'area del quadrato costruito sul cateto maggiore.

La dimostrazione di Garfield

Una dimostrazione geometrica fu trovata nel 1876 da James Abraham Garfield, che in seguito divenne il ventesimo Presidente degli Stati Uniti.

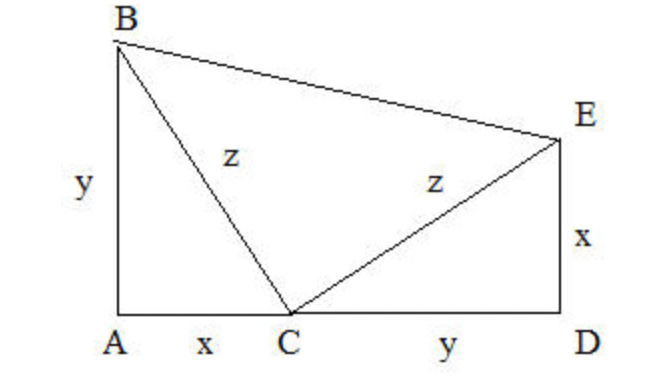
http://rudimatematici-lescienze.blogautore.espresso.repubblica.it/2009/04/15/il-teorema-di-pitagora/

Sia ABC il nostro triangolo; su di esso costruiamo il triangolo CDE (uguale ad ABC e con CD prosecuzione di AC) e il triangolo BCE che risulta per costruzione isoscele (per costruzione, i lati BC e CE sono uguali).

In sostanza, abbiamo una cosa come in figura.

Ora, considerato che l'angolo in A è retto, si ha che è ACB+ECD=90°, in quanto angoli interni non retti di triangoli rettangoli uguali; da questo, si ha che per costruzione è BCE=90°.

Consideriamo ora il trapezio di basi BA e ED. La sua area vale:

S = (x+y) * (x+y) / 2 = (x+y)^2 / 2

Ma quest'area deve essere uguale alla somma delle aree dei tre triangoli che formano il trapezio:

S = x*y / 2 + z^2 / 2 + x*y / 2 = (z^2 + 2xy) / 2

Uguagliando le due aree e moltiplicando ambo i termini per 2:

(x+y)^2 = z^2 + 2xy

x^2 + y^2 + 2xy = z^2 + 2xy

x^2 + y^2 = z^2

Q.E.D.

Esistono e si trovano in rete esempi di dimostrazioni fisiche del Teorema.

Incommensurabili

Consideriamo un triangolo rettangolo isoscele con i cateti di lunghezza 1: il teorema ci conferma che l'ipotenusa misurerà la radice quadrata di 2: il rapporto fra la diagonale e il lato di un quadrato non può essere espresso con un numero intero.

Non esiste cioè un sottomultiplo comune ad entrambi: diagonale e lato del quadrato sono incommensurabili.

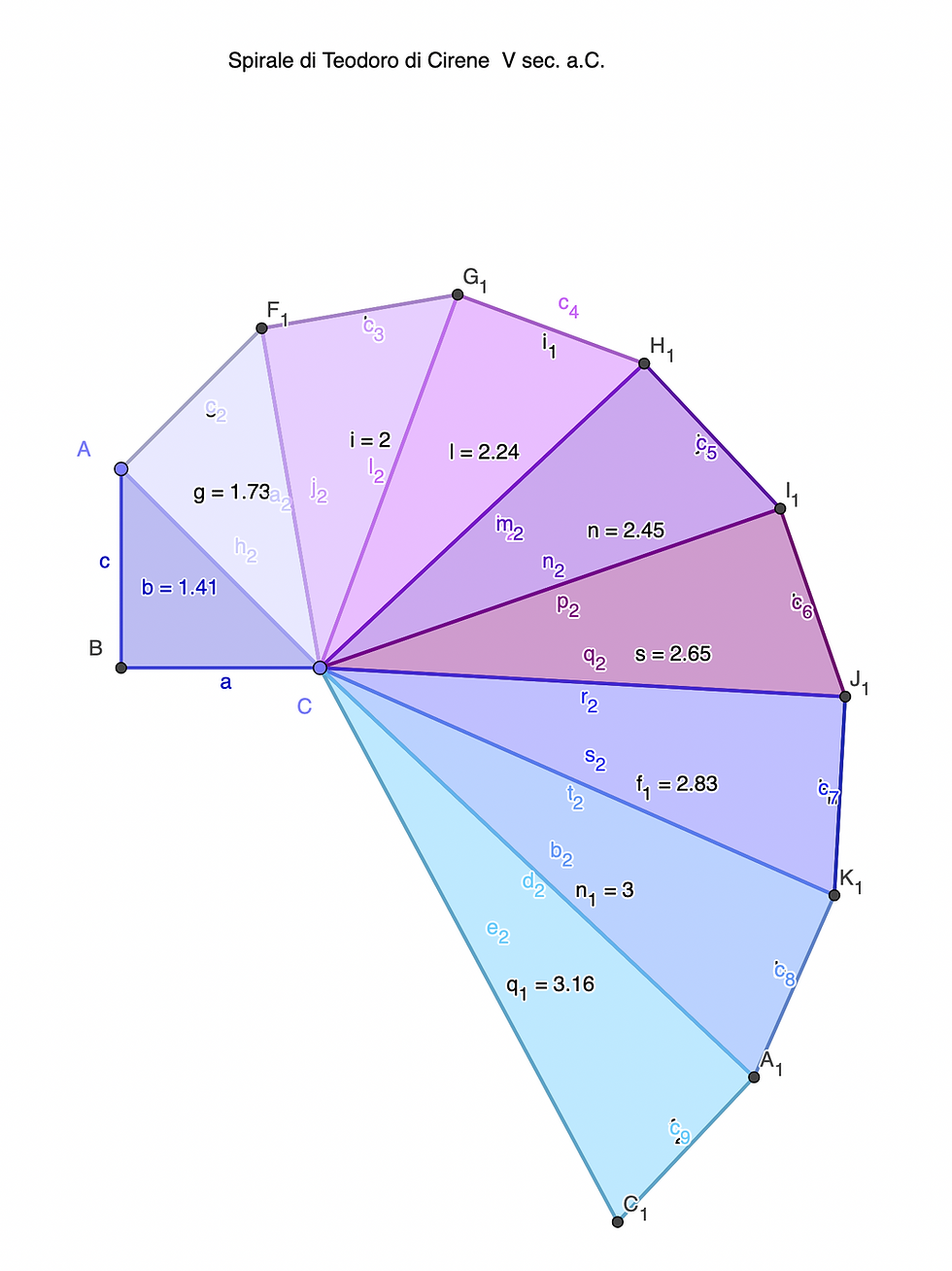
Questa scoperta rappresentò una vera tragedia per i Pitagorici.

Per alcuni storici ciò avrebbe potuto rappresentare il crollo della filosofia pitagorica.

Tutto questo non mise certo in dubbio la fiducia nella ragione tra i Pitagorici, tanto è vero che altri Autori sostengono che i Pitagorici erano perfettamente in grado di concepire il numero reale, pur continuando a dare al termine numero il significato di numero intero.

Aristotele afferma che la dottrina di Platone è puramente e semplicemente quella dei Pitagorici, cui avrebbe cambiato solo una parola, scrivendo "idee" invece che "numeri".

Il Teorema di Pitagora vale indipendentemente dal poligono regolare costruito sui lati del triangolo rettangolo?

Dopo aver verificato il teorema di Pitagora in contesti tradizionali possiamo riflettere sulla possibilità che il Teorema possa essere verificato anche costruendo altri poligoni regolari, oltre il quadrato, su cateti e ipotenusa.

La costruzione di GeoGebra ci conferma quanto riportato nella domanda.

Fermat e il Teorema

La storia della matematica ci attesta che il matematico Pierre de Fermat, vissuto nel '600, si era chiesto se esistessero soluzioni intere positive dell’equazione x^n + y^n = z^n quando n è maggiore di 2.

Scrisse di avere risolto la sua congettura ma non se ne trovò mai la dimostrazione.

Fu il matematico britannico André Weils, oltre 300 anni dopo, nel 1994, a dimostrare che non esistono soluzioni intere positive se l'esponente è un intero maggiore di 2.

E' sempre valido il Teorema di Pitagora? Oltre la geometria euclidea

Bibliografia

Vite dei filosofi Diogene Laerzio 2000 Laterza ed.

L'arte della matematica Simone Weil, André Weil 2018 Adelphi

Il teorema del pappagallo Denis Guedj 2000 Longanesi

Storia della matematica Carl B. Boyer 1980 Oscar Mondadori