keplero superstar
- Claudio Carabelli

- 8 apr 2019
- Tempo di lettura: 11 min
La macchina planetaria di Keplero: l’Astronomia dialoga con la Geometria (Mysterium cosmographicum, 1596)
prof. Carabelli Claudio
Introduzione
Questo progetto, da realizzare in Atelier digitale, consente una triplice lettura: è rivolto agli studenti del 3^ anno della Secondaria di 1^ grado, semplificando i calcoli relativi ai poliedri (a titolo dimostrativo si proporranno le formule per ricavare i raggi della sfera inscritta, circoscritta e lo spigolo del cubo nel caso Saturno/Giove, proponendo la lettura degli Elementi di Euclide, libro XIII prop. XV); può essere rivolto agli studenti del biennio nella sua globalità; può rappresentare, con i dovuti approfondimenti storico-matematici-astronomici, un corso di formazione per docenti di disciplina della Secondaria.
Il progetto accompagnerà gli allievi dentro un percorso di storia dell’Astronomia (Mysterium cosmographicum, 1596) e della Matematica (Elementi di Euclide; poliedri regolari).
Verrà introdotta la progettazione CAD (Fusion 360) nelle sue linee essenziali e la stampa 3D (Wanhao D9 300, Cura) con l’obiettivo finale di costruire il modello planetario di Keplero.
Keplero nel Mysterium, saggio scientifico scritto a 25 anni, espone l’idea che il numero dei pianeti e la loro reciproca distanza non sia casuale ma riconducibile ad una relazione esistente con i 5 poliedri regolari: in pratica ogni sfera (orbe) riferita ad un pianeta è circoscritta ad uno specifico poliedro (i vertici del poliedro sono punti della sfera) e inscritta ad un altro (la sfera è tangente ai centri delle facce del poliedro).
Keplero stesso confrontando la propria ricerca matematica con i dati astronomici osservati si renderà conto della fallacia della propria idea guida. Ma da questa opera giovanile prenderà spunto una riflessione più vasta e profonda che lo porterà negli anni a comprendere meglio i meccanismi con cui si svolgono i fenomeni celesti e a formulare le proprie leggi.
Questo fatto farà ulteriormente riflettere gli studenti sul significato dell’errore, sempre foriero di nuova conoscenza.
Dedicato a Graziano Tinivella, compagno di Liceo all’E.Fermi di Arona
19 luglio 1595, l'intuizione
Keplero è in classe e sta disegnando sulla lavagna un elaborato schizzo geometrico che tenta di spiegare i meccanismi della congiunzione fra i pianeti più esterni, Saturno e Giove, che accade ogni ottocento anni, nel triangolo formato nello Zodiaco dalle tre costellazioni di Ariete, Leone e Scorpione. Per spiegare questo evento, Keplero comincia così a disegnare una struttura formata da dei triangoli non perfettamente equilateri, che rappresentano le «congiunzioni maggiori di Giove e Saturno», inscritti nella circonferenza dello Zodiaco. La struttura genera una seconda circonferenza, al centro di quella maggiore, in questo modo:

Subito un fatto appare all’occhio di Keplero: «Il rapporto dei cerchi tra di loro mi risultò, visivamente, quasi lo stesso che vi è tra Saturno e Giove; e il triangolo è la prima tra le figure, così come Saturno e Giove sono i primi pianeti». Il rapporto tra i raggi dei due cerchi si avvicina molto a quello esistente tra le distanze di Giove e Saturno dal centro dell’universo. Keplero cerca allora di continuare l’analogia prendendo in considerazione anche Marte, ma senza successo. L’idea che vi possa essere una correlazione tra i poligoni regolari inscritti in una circonferenza e le distanze dei pianeti dal Sole è però troppo affascinante per Keplero, e lo stimola a battere ancora quella strada.
Si è posto da tempo alcune domande:
• Perché questo numero dei pianeti (allora 6 pianeti conosciuti)?
• Perché questa disposizione (distanza)?
• Perché questi moti (velocità)?
Per noi oggi le prime due domande sono senza senso e la nostra attenzione scientifica si fisserebbe solo sulla terza.
Keplero invece è convinto che Dio abbia inserito un ordine, un’armonia nell’Universo e che ogni cosa quindi ha la propria ragione d’essere. Il suo obiettivo è conoscere meglio la mente di Dio attraverso le sue opere (non vi suona familiare come l’intento identico di un famoso musicista e di un illustre scienziato del Settecento?).
Nel M.C. Keplero prende coraggiosamente (quanto è lontano Campo dei Fiori da Graz/Tubinga?) posizione nella disputa sui Massimi sistemi del mondo, descrivendo la superiorità del sistema copernicano rispetto a quello tolemaico, perché a suo dire descrive e spiega il moto dei pianeti non solo matematicamente, ma anche fisicamente; inoltre il modello copernicano rispetta meglio la natura che opera sempre investendo sulla semplicità e sull’unità.
“Copernico sta a Tolomeo come la realtà all’apparenza” avrà modo di confidare.
Scrive della necessità di passare da una astronomia di posizione (osservo e interpreto), all’astrofisica (modello che prevede) e manifesta l’esigenza di confrontare sempre le proprie ipotesi con i dati sperimentali.
il predestinato

In primo luogo,
Keplero ricerca eventuali leggi numeriche che diano ragione della posizione dei pianeti: calcola cioè se i raggi dei pianeti sono multipli tra loro o se sussiste analoga relazione.
A fronte dell’insuccesso di questa idea comincia a pensare che il linguaggio ideale con cui confrontarsi non sia quello dell’aritmetica ma quello della geometria.
Probabilmente gli fa da guida l’analogia con l’idea molto diffusa all’epoca e dovuta a Nicola da Cusa

che assegnava alla sfera il significato di rappresentare la Trinità e la creatura umana nel suo insieme: Dio è il centro della sfera, Cristo ne rappresenta la superficie, mentre lo Spirito Santo ne occupa il volume; una freccia che definisce il raggio rappresenta l’uomo e il cerchio massimo che essa descrive è l’emblema dell’anima.
Per Keplero le analogie sono strumenti per indagare, con l’aiuto della immaginazione, la natura.
La sua ricerca lo porta a considerare eventuali relazioni fra il Sistema Solare e le figure geometriche.
Prova quindi a mettere in relazione le distanze dei pianeti dal Sole e i poligoni regolari inscritti e circoscritti ad una Circonferenza.
Riflette anche sul fatto che tali poligoni sono infiniti mentre i pianeti sono solo sei.
A questo punto decide di abbandonare la geometria piana e investigare quella solida: dai poligoni ai poliedri, dalla Circonferenza alla sfera.
Immagina,
allora un sistema ad incastro in cui le sfere (allora: gli orbi) che rappresentano le orbite dei pianeti e sostengono i pianeti stessi, sono alternate ai 5 poliedri regolari.
Nel dettaglio: sfera di Saturno-cubo, sfera di Giove-tetraedro, sfera di Marte-dodecaedro, sfera della Terra-icosaedro, sfera di Venere-ottaedro, sfera di Mercurio e al centro il Sole.
Progettazione e costruzione
Progettiamo e costruiamo la sfera (orbe) di Saturno,
la stampante 3D Wanhao D9 300 ha nella propria peculiarità il suo limite: la sfera riferita a Saturno non potrà avere il diametro superiore a 30 cm.
In realtà poiché, per costruzione, è previsto un ulteriore anello che espande tale sfera fisseremo tale diametro esterno pari a 26.3 cm e quello interno pari. 25.3 cm.
Le dimensioni di ogni ulteriore sfera e quelle dei 5 poliedri regolari deriveranno conseguentemente da questo valore limite.
Apriamo quindi il software Fusion 360 e progettiamo tale sfera.
Con lo strumento “cerchio” si disegnano due cerchi concentrici, rispettando i valori predetti per il diametro; per sottrazione otteniamo la corona circolare che verrà estrusa per 5 mm.
A questo punto si progetta la sfera, la si svuota con il comando “shell “e si ricava una semisfera.
Quale spessore dovrà avere la sfera (orbe) di Saturno?
Questo è un punto teorico, prima ancora che fisico, fondamentale che ci riporta ancora a Keplero e al suo Mysterium.
Pur considerando le orbite dei pianeti come circonferenze (Keplero, rinunciando alle circonferenze opterà in seguito per le orbite ellittiche; Galileo rimarrà invece fedele a questa tradizione che risaliva a Platone e al De Caelo di Aristotele, forse anche a causa delle proprie convinzioni estetiche, così come suggerito nel saggio magistrale “Galileo critico delle arti”, scritto dal critico d’arte Panofskj), gli astronomi del Cinquecento erano ben consci dell’eccentricità di tali curve; se i dati sperimentali avessero confermato le orbite circolari, lo spessore degli orbi sarebbe stato infinitesimale.
Per spiegare l’eccentricità si supponeva quindi che le calotte sferiche (gli orbi) avessero uno spessore diverso e per quanto possibile proporzionale all’eccentricità del pianeta (valori massimi per Saturno e Mercurio).
Quindi lo spessore della nostra sfera di Saturno è posto uguale a 5 mm; per questo motivo il diametro interno sarà uguale a 25.3 mm.
Nelle immagini seguenti vengono riportati anche i parametri utilizzati con Cura, software che utilizziamo per trasformare il file di Fusion 360 (.stl) in un formato (.gcode) che sarà riconoscibile dalla stampante 3D.
Per la stampa degli orbi utilizzeremo PETG blu trasparente; per i poliedri verrà utilizzato PLA verde acqua.
Progettiamo, costruiamo e stampiamo il Cubo o Esaedro
Dagli Elementi di Euclide

Euclide nel XIII ed ultimo libro degli Elementi ci insegna come sia semplice, conoscendo il diametro di una sfera, ricavare lo spigolo del cubo inscritto.
È sufficiente applicare il teorema di Pitagora e quindi una conoscenza alla portata degli allievi di classe 3^ della Secondaria di 1^ grado.
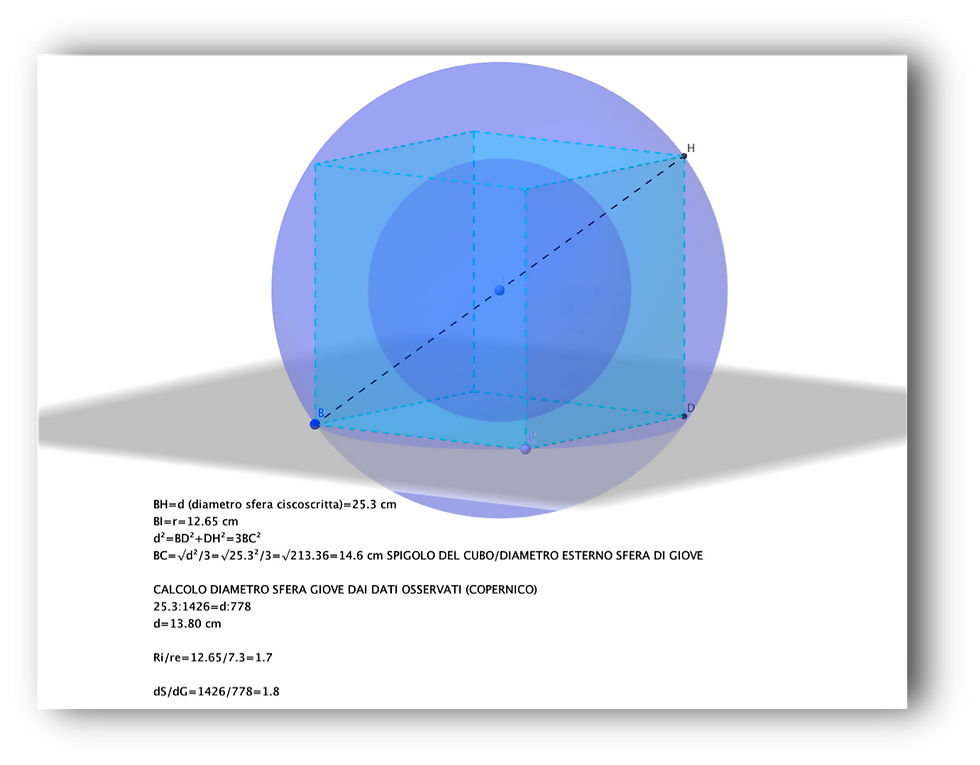
I nostri calcoli ci consentono di ottenere lo spigolo del cubo inscritto nella nostra sfera di Saturno pari a 14.6 cm.
Procediamo allo stesso modo: costruiamo il Cubo e poi, con il comando “shell”, lo svuotiamo, mantenendo lo spigolo di 5 mm.
La parte che si intravvede tra gli spigoli del cubo rappresenta il sostegno alla stampa; alla fine verrà eliminato.
Il diametro della sfera inscritta al cubo (orbe di Giove) è uguale alla misura dello spigolo, per cui il suo raggio misura 7.3 cm.
A questo punto calcoliamo il rapporto tra il raggio della sfera di Saturno (interno) e quello esterno della sfera di Giove: 1.726.
Keplero, partendo dai dati in suo possesso (che sono i dati di Copernico, quindi desunti dal De Revolutionibus, 1543) calcola il rapporto fra le distanze dal Sole di Saturno e Giove (per noi oggi 1426/778 Mkm) e trova il valore 1.83!
Questo valore osservato è diverso, ma non troppo da quello calcolato matematicamente a partire dal raggio della sfera circoscritta/inscritta al cubo.
Per Keplero si tratta di una prima conferma della sua idea.
Ma l’astronomo è molto puntiglioso e pur proseguendo calcoli e osservazioni sui successivi poliedri/pianeti, comincia a chiedersi il perché di questa discrepanza fra i numeri.
Nel capitolo XIX del M.C. Keplero ci informa che l’immensa distanza di Saturno dalla Terra è sicuramente causa di errori nella osservazione.
Cita il fatto che nell’inverno precedente, novembre 1594, Saturno è stato osservato esattamente nel cuore del Leone, posizione in cui avrebbe dovuto trovarsi invece tra il 21/31 ottobre precedente, con una differenza di longitudine pari a 37’.
Progettiamo e costruiamo la sfera (orbe) di Giove,
torniamo al nostro modello e ora, conoscendo la distanza di Giove dal Sole, con una semplice proporzione possiamo ricavarci quale dovrà essere il diametro esterno della sfera di Giove, che sarà la prossima ad essere progettata e stampata: 13.80 cm.
Confermiamo lo spessore di tale sfera in 5 mm: il suo diametro interno vale quindi 12.80 cm.
Progettiamo, costruiamo e stampiamo il Tetraedro,
Dagli Elementi di Euclide,

La misura dello spigolo del Tetraedro lo si ricava da Euclide con la formula descritta nella Proposizione 13:
L = 2/3 xV6 xR (raggio interno della sfera circoscritta).
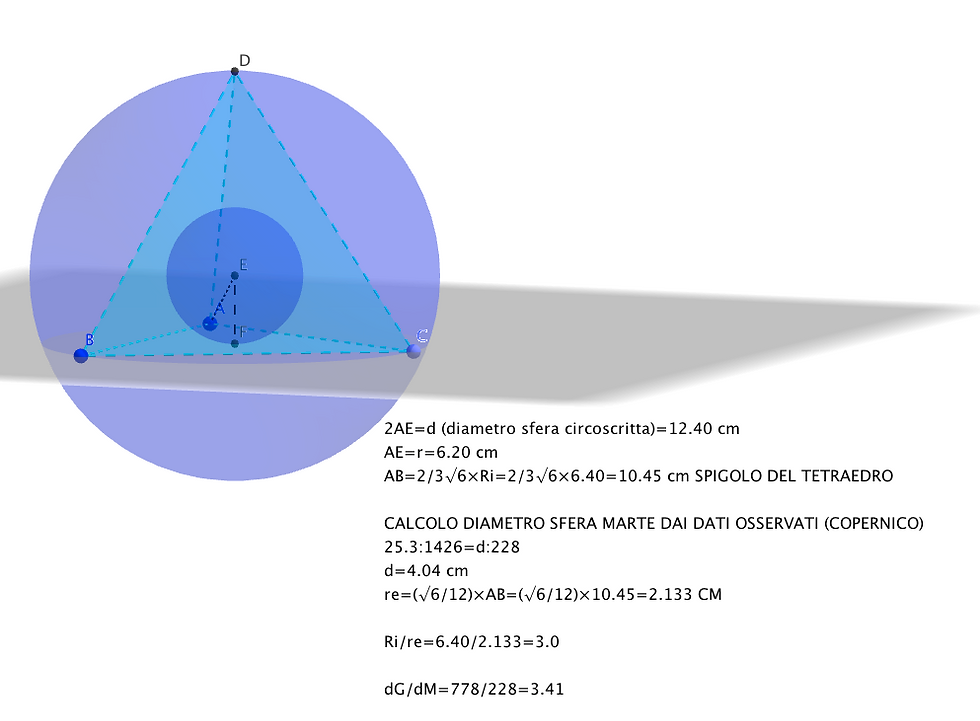
Pertanto lo spigolo misura 10.45 cm.
Procediamo allo stesso modo: progettiamo il Tetraedro e poi, con il comando “shell”, lo svuotiamo, mantenendo lo spessore dello spigolo di 5 mm.
Il raggio della sfera inscritta al Tetraedro (orbe di Marte) si ricava dalla formula L x V6/12, (dove L = spigolo Tetraedro) per cui il suo raggio misura 2.133 cm.
A questo punto calcoliamo il rapporto tra il raggio interno della sfera di Giove e quello esterno della sfera di Marte: 3.00.
Keplero, partendo dai dati in suo possesso calcola il rapporto fra le distanze dal Sole di Giove e Marte (per noie oggi 778/228 Mkm) e trova il valore 3.41!
Questo valore osservato,, da un lato giustifica perché Keplero, dopo il Cubo, abbia inserito proprio il Tetraedro (per gli altri 3 poliedri regolari il valore calcolato sarebbe molto più basso) tra le orbite di Giove e Marte, dall’altro lascia perplesso lo stesso Autore che nel cap. XIV si chiede il perché di tanta esuberanza da parte della Natura. “Quanto è inutile questo spazio vuoto...”, lasciando intuire la possibilità della esistenza di un altro corpo celeste (che in effetti esiste: la fascia degli asteroidi), possibilità che però scarta in quanto non conforme alla sua ipotesi dei 5 poliedri regolari.
Progettiamo e costruiamo la sfera (orbe) di Marte
Torniamo al nostro modello e ora, conoscendo la distanza di Marte dal Sole, con una semplice proporzione possiamo ricavarci quale dovrà essere il diametro esterno della sfera di Marte, che sarà la prossima ad essere progettata e stampata: 4.04 cm.
Confermiamo lo spessore di tale sfera in 2 mm: il suo diametro interno vale quindi 3.64 cm.
Progettiamo, costruiamo e stampiamo il Dodecaedro
Dagli Elementi di Euclide:

La misura dello spigolo del Dodecaedro lo si ricava da Euclide con la formula descritta nella Proposizione 17:
L = AB = 4 * R (raggio interno sfera circoscritta)/V3 * (1+V5)
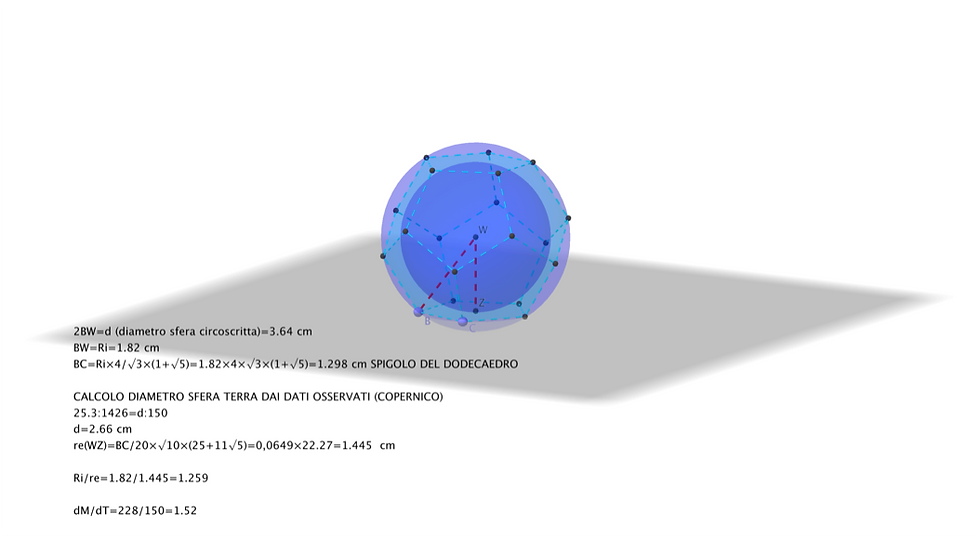
Pertanto lo spigolo misura 1.298 cm.
Procediamo allo stesso modo: progettiamo il Dodecaedro e poi, con il comando “shell”, lo svuotiamo, mantenendo lo spessore dello spigolo di 2 mm.
Il raggio della sfera inscritta al Dodecaedro (orbe della Terra: Grande orbe) si ricava dalla formula L x VV10 * (25 + 11V5)/20, (dove L = spigolo Dodecaedro) per cui il suo raggio misura 1.445 cm.
A questo punto calcoliamo il rapporto tra il raggio interno della sfera di Marte e quello esterno della sfera della Terra: 1.259.
Keplero, partendo dai dati in suo possesso calcola il rapporto fra le distanze dal Sole di Marte e la Terra (per noi oggi 228/150 Mkm) e trova il valore 1.52!
Keplero tenta di giustificare tale differenza ragionando sul fatto di considerare o meno come un corpo unico il “blocco” Terra/Luna.
Progettiamo e costruiamo la sfera (orbe) della Terra,
Torniamo al nostro modello e ora, conoscendo la distanza della Terra dal Sole, con una semplice proporzione possiamo ricavarci quale dovrà essere il diametro esterno della sfera della Terra, che sarà la prossima ad essere progettata e stampata: 2.66 cm.
Confermiamo lo spessore di tale sfera in 2 mm: il suo diametro interno vale quindi 2.26 cm.
Progettiamo, costruiamo e stampiamo l’Icosaedro
Dagli Elementi di Euclide:

La misura dello spigolo dell’Icosaedro lo si ricava da Euclide con la formula descritta nella Proposizione 16:
L = AB = 4 * R (raggio interno sfera circoscritta )/(VV10+2V5)
Pertanto lo spigolo misura 1.188 cm.
Procediamo allo stesso modo: progettiamo l’Icosaedro e poi, con il comando “shell”, lo svuotiamo, mantenendo lo spessore dello spigolo di 2 mm.
Il raggio della sfera inscritta all’Icosaedro (orbe di Venere) si ricava dalla formula L x VV3 * (3 + V5)/12, (dove L = spigolo dell’Icosaedro) per cui il suo raggio misura 0.898 cm.
A questo punto calcoliamo il rapporto tra il raggio interno della sfera della Terra e quello esterno della sfera di Venere: 1.258.
Keplero, partendo dai dati in suo possesso calcola il rapporto fra le distanze dal Sole di Terra e Venere (per noi oggi 150/108 Mkm) e trova il valore 1.38!
La differenza osservata è imputabile, secondo l’astronomo, al fatto che la superficie di Venere è ricoperta da spesse coltri di nuvole che riflettendo la luce solare determinano una difficile osservazione del pianeta.

Progettiamo e costruiamo la sfera (orbe) di Venere
Torniamo al nostro modello e ora, conoscendo la distanza di Venere dal Sole, con una semplice proporzione possiamo ricavarci quale dovrà essere il diametro esterno della sfera di Venere, che sarà la prossima ad essere progettata e stampata: 1.92 cm.
Lo spessore di tale sfera sara solo di 1 mm: il suo diametro interno vale quindi 1.72 cm.
Progettiamo, costruiamo e stampiamo l’Ottaedro
Dagli Elementi di Euclide:

La misura dello spigolo dell’Ottaedro lo si ricava da Euclide con la formula descritta nella Proposizione 14:
L = AB = V2 * R (raggio interno sfera circoscritta)
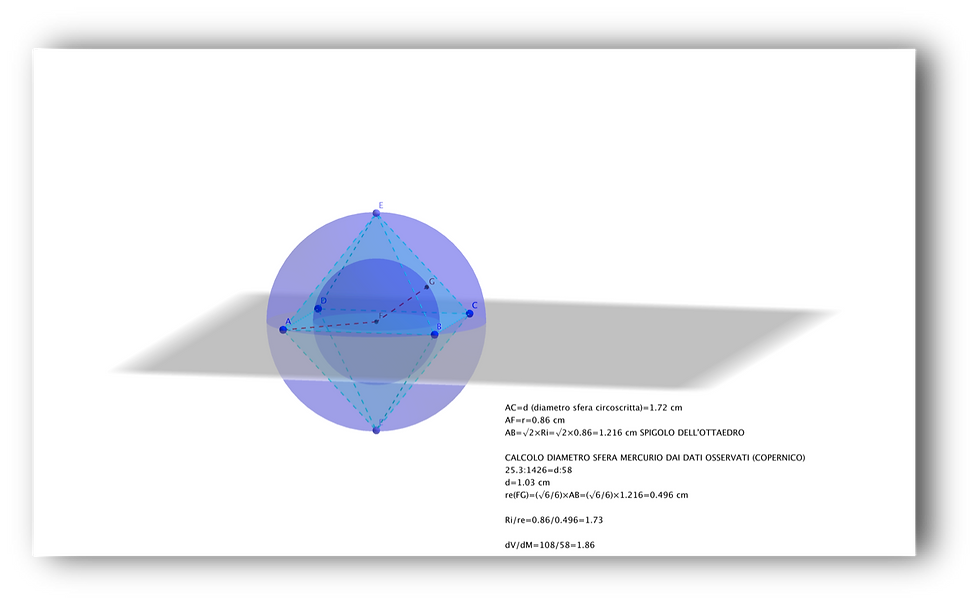
Pertanto lo spigolo misura 1.216 cm.
Procediamo allo stesso modo: progettiamo l’Ottaedro e poi, con il comando “shell”, lo svuotiamo, mantenendo lo spessore dello spigolo di 1 mm.
Per comodità di costruzione progettiamo un tetraedro e poi lo stamperemo due volte.
Il raggio della sfera inscritta all’Ottaedro (orbe di Mercurio) si ricava dalla formula L x V6/6, (dove L = spigolo dell’Ottaedro) per cui il suo raggio misura 0.496 cm.
A questo punto calcoliamo il rapporto tra il raggio interno della sfera di Venere e quello esterno della sfera di Mercurio: 1.73
Keplero, partendo dai dati in suo possesso calcola il rapporto fra le distanze dal Sole di Venere e Mercurio (per noi oggi 108/58 Mkm) e trova il valore 1.86!
L’astronomo imputa questa differenza all’estrema difficoltà nell’osservazione del pianeta Mercurio che solo in rari momenti è visibile sullo sfondo del Sole.
Progettiamo e costruiamo la sfera (orbe) di Mercurio
Torniamo al nostro modello e ora, conoscendo la distanza di Mercurio dal Sole, con una semplice proporzione possiamo ricavarci quale dovrà essere il diametro esterno della sfera di Mercurio, che sarà l’ultima ad essere progettata e stampata: 1.03 cm.
Lo spessore di tale sfera sara solo di 1 mm: il suo diametro interno vale quindi 0.83 cm.
Parametri riassuntivi

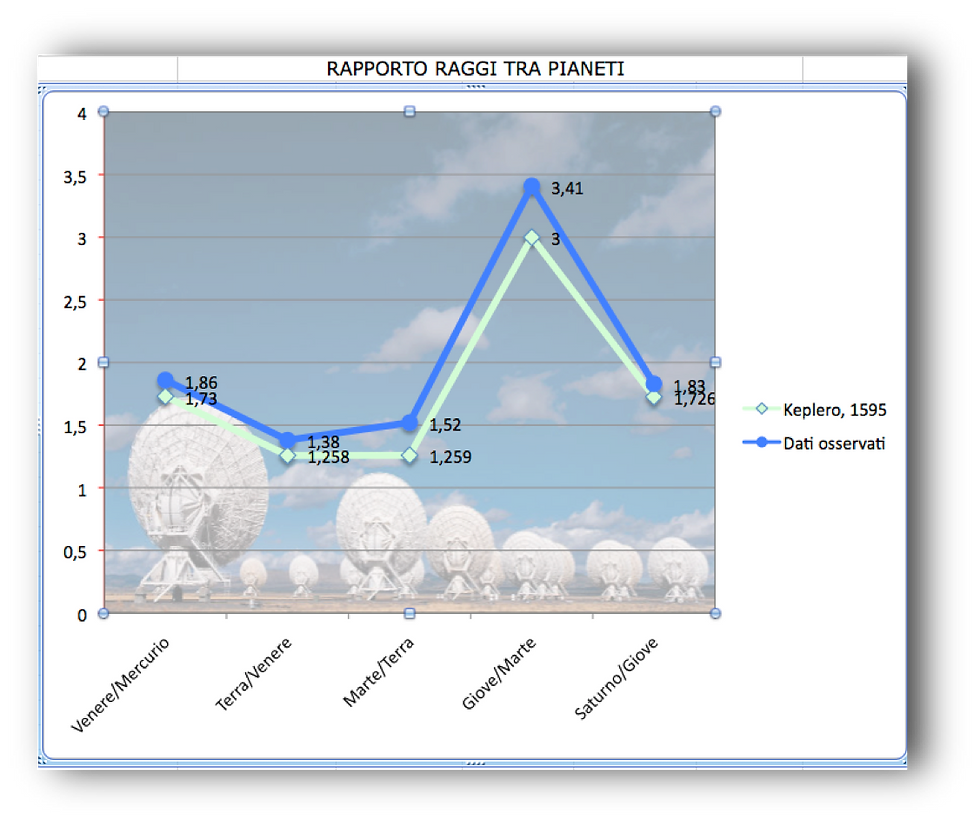
Conclusioni
A fronte di queste discordanze Keplero osa dapprima mettere in discussione le osservazioni di Copernico e successivamente, accordatosi con il vecchio maestro Maestlin, che rifarà tutti i calcoli, ricalcolerà le distanze dei pianeti e relative eccentricità non più a partire dalla posizione vera del Sole ma da un punto definito come Sole medio.
Anche dopo questo aggiornamento le differenze permangono e Keplero si arrende all’evidenza.
Nel capitolo XVIII Keplero scrive:
Ceux donc qui veulent examiner toutes choses avec beaucoup d’exactitude estimeront, puisque le calcul à partir des corps ne correspond pas rigoureusement aux opinions de Copernic et à ses valeurs, que tout non travail n’a été qu’n jeu. Et à moins que je ne résiste là contre, j’aurai perdu ma cause en vertu de ma propre sentence.
Negli ultimi capitoli del Mysterium Keplero investiga le velocità dei pianeti, riflettendo sul fatto che queste siano differenti non solo tra i diversi pianeti ma anche, per uno stesso pianeta, nell’ambito della propria orbita. Causa di questi moti è il Sole, meglio la sua “virtù” (forza motrice).
E questa riflessione finale, per ora ancora in bozza, rappresenta certamente il grande contributo scientifico del Mysterium.
Comunque entusiasta del proprio modello Keplero inserisce una tavola III che mostra le dimensioni e le distanze degli orbi dei pianeti nel mezzo dei cinque corpi regolari della geometria.
Viene dedicata al principe Federico, duca del Wurtemberg che, sedotto dall’immagine, decide di fare costruire un “Kredenzbecher”.
In realtà questa coppa non verrà mai realizzata dal duca.
Senza alcuna pretesa di “perfezione”, tenteremo ora l’impresa con le tecnologie moderne.
Assemblaggio
Bibliografia
Johannes Kepler Le secret du monde (Mysterium cosmographicum).
Ed. Gallimard, 1993
Massimo Bucciantini Galileo e Keplero. Filosofia, cosmologia e teologia nell’Età della Controriforma.
Einaudi, 2003
Erwin Panofsky Galileo as a Critic of The Arts.
Aabscondita, 2008
Gabriele Uggias Keplero e la musica. Dottorato di ricerca
Alma Mater Studiorum 2015
Anna Maria Lombardi Keplero (collana I grandi della Scienza) .
Le Scienze, 2000.
Euclide Gli Elementi.
UTET, 1996
Strumenti
Fusion 360, CAD
Stampante 3d Wanhao D9 300 MK1
Cura (software)
GeoGebra5
Atelier digitale creativo Ungaretti (IC Ungaretti di Sesto Calende)
Sesto Calende, aprile 2019














































































Commenti