L'incertezza della misura e la matematica di strada.
- Claudio Carabelli

- 20 mag 2019
- Tempo di lettura: 3 min

Durante la prima fase della Rivoluzione francese, l'8 maggio del 1790 Talleyrand propose all'Assemblea Costituente, su suggerimento di una commissione dell'Accademia delle Scienze, l'adozione di un grande progetto collettivo: un sistema unificato di pesi e misure.
Il progetto doveva rispondere a tre obiettivi principali:
a. il sistema doveva essere uniforme, cioè doveva fare riferimento alla divisione decimale per tutte le differenti misure (pesi, aree, di lunghezza e dei volumi)
b. il sistema doveva presentare un'economia intellettuale e collegare tra loro le unità prescelte, di modo che l'unità di lunghezza determinasse le altre, ad eccezione dell'unità di tempo
c. l'unità di lunghezza doveva essere ricavata dalla natura, in modo da essere accettata da tutti i popoli della terra.
La misura del meridiano terrestre, effettuata da due Commissioni (una con a capo l'astronomo Mèchain, l'altra affidata al Delambre), fu un evento epico, sia per il metodo e gli strumenti utilizzati, triangolazioni e cerchio ripetitore di Borda, sia per gli eventi bellici entro i quali si svolse.
Un decennio dopo, nel 1799, la Commissione Internazionale ratificò la misura, facendo costruire il campione di platino-iridio: il metro veniva definito come la 40 milionesima parte del meridiano terrestre.
La stima fatta nel 1980 (misura effettuata da satelliti) della distanza Dunkerque-Barcellona differisce dal valore ottenuto da Delambre e Méchain di 10 metri cioè con un errore inferiore allo 0,001%.
Il risultato della misurazione di una grandezza fisica non è mai un ben definito valore numerico, bensì sempre un intervallo di valori. Ciò significa che la misura è sempre caratterizzata da incertezza.
Cause di incertezza possono essere riferite alle caratteristiche (risoluzione) dello strumento di misura, alla relazione strumento-oggetto da misurare, relazione soggetto-oggetto da misurare, errori di allineamento ed altro.
Inoltre non va dimenticata l'incertezza relativa alle misure indirette.
Pensando a una ricaduta didattica dell'argomento (auspicabile la rivisitazione del contesto storico) mi sono ricordato di una constatazione scritta anni fa da Bruno D'Amore:
"Il mondo della matematica che si apprende aI scuola è spesso fatto di stereotipi. La maggior parte delle attività (a qualsiasi livello scolastico) è una massa di meccanismi all'apparenza inutili che sembrano non aver capo né coda (in realtà non è vero, ma molti ragazzi la pensano così). Perché nella scuola media, per esempio, insegnanti e allievi (e dunque: società) debbano perdere tempo (e dunque: denaro pubblico) a effettuare calcoli inutili e ripetitivi come quelli di bizzarre espressioni, è un bel mistero!"
Anni di esperienza sul campo mi consentono di affermare che il problema è ben noto e che tanti colleghi si prodigano quotidianamente per proporre agli allievi attività laboratoriali che consentano di far apprendere in modo coinvolgente, sedimentando negli studenti conoscenze e abilità che si tradurranno in modelli cognitivi appropriati.
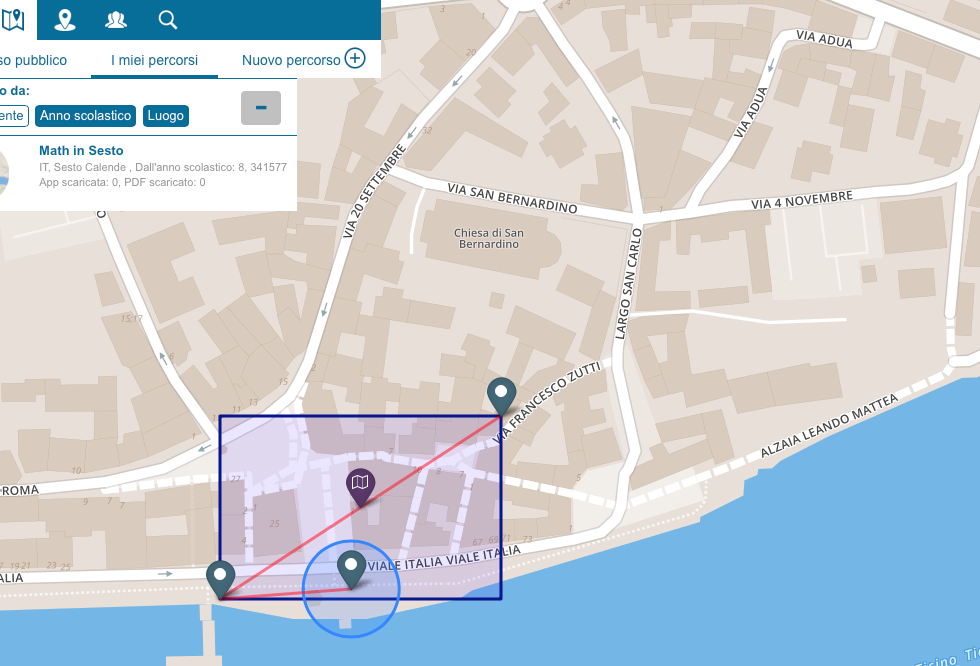
Quella che qualcuno ha definito "matematica di strada" (vi ricordate "Learning maths outdoor" degli anni '80?) è un'idea rivisitata oggi da MathCityMap, che integra quella proposta con le nuove tecnologie (smartphone con sistema GPS e tablet) che la attuano (offrendo la possibilità di condividere l'attività).
Il fare matematica si integra con l'aspetto transdisciplinare e ludico.
MathCityMap (MCM) è un progetto del gruppo di lavoro Matis I (Univ. Goethe - Francoforte) in collaborazione con l’università di Potsdam, che coniuga l’idea di passeggiata matematica con le nuove tecnologie basate sul Web.
Gli studenti possono o progettare nuovi percorsi o usufruire di quelli esistenti.
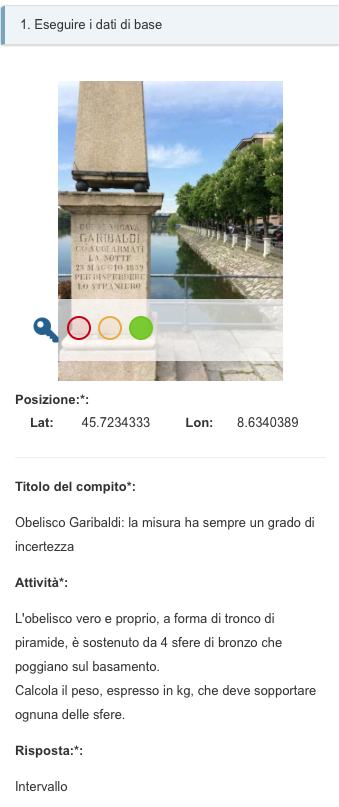
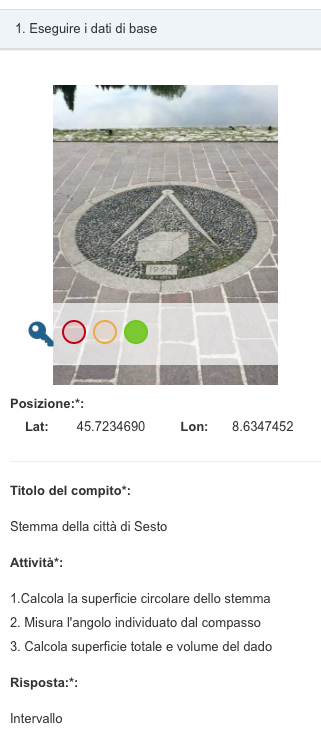
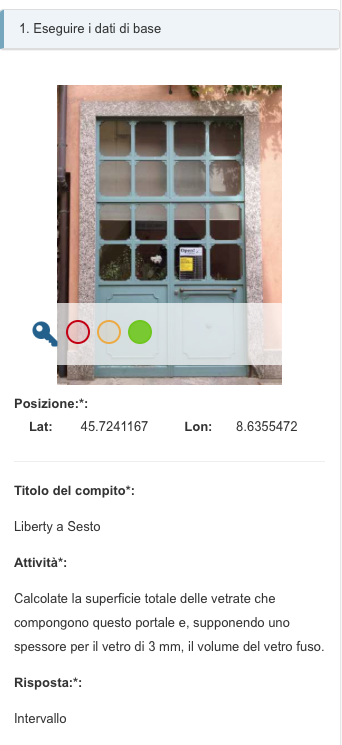
Alla base di ogni attività vi è la misura: pur chiedendo la massima precisione possibile nell'uso degli strumenti, per quanto sovraesposto, si dà la possibilità di accettare valori all'interno di un intervallo definito in anticipo.
L'accettazione o meno del valore registrato da parte dell'algoritmo matematico di MCM farà riflettere gli studenti sull'incertezza insita nella misura.
Qualsiasi evento didattico-educativo rappresenta un’azione condivisa per cercare uno scambio di significati e di emozioni tra alunno e docente. Ogni volta che alunno e docente riescono a concordare e condividere il significato di un’unità di conoscenza si verifica un apprendimento significativo.








Commenti