Ombre: a cavallo di un raggio di luce

Le Muse inquietanti, 1918 Giorgio De Chirico

"L’illuminazione netta e intensa, come in tutte le opere metafisiche, arriva da destra e segna profonde ombre ritagliate sul palcoscenico verso sinistra".

Le ombre riflettono la forma degli oggetti, tanto realistici che astratti.

Diversi anni fa, a luglio del 1989, vagabondando lungo il Quai du Louvre, intento a curiosare tra le bancarelle verdi (Bouquinistes) che vendono libri antichi e usati e che ancora oggi, dopo secoli, costituiscono un elemento caratteristico del lungosenna, lo sguardo cadde su un volumetto dal titolo in italiano: si trattava dell'Ottica di Euclide, il classico manuale Hoepli, commentata dal prof. Giuseppe Ovio, pubblicato nel 1918.

Lo acquistai e leggendo la prefazione, attribuita a Teone di Alessandria, mi chiesi se fosse stato il mio occhio ad avere "visto" il piccolo manuale o viceversa non fosse stato il raggio di luce proveniente da esso a colpire il mio occhio.

Stiamo parlando della teoria della visione: Euclide nel I libro dell'Ottica sostiene, errando, che i raggi visivi partirebbero dall'occhio e raggiungerebbero gli oggetti, teoria sostenuta più tardi anche da Epicuro e Galeno.

Ai tempi di Euclide (IV/III sec. a.C.) rappresentava la teoria moderna della visione, perché più antica, risalente a Democrito, era la teoria degli efflussi emanati dagli oggetti e giungenti all'occhio.

Scrive Teone riferendosi a Euclide:

... e dettava essere i raggi emanati dalle sorgenti di luce che stanno in nostro possesso, la cagione che dei corpi opposti a tali sorgenti, parte rimane illuminata, parte getta ombre. Queste ombre sono talvolta eguali ai corpi che le determinano, talvolta maggiori, talvolta minori; e precisamente ombre eguali darebbero i corpi che sono eguali alla sorgente, giacché i raggi estremi decorrono paralleli; mentre minori dei corpi sono le ombre quando le sorgenti luminose sono maggiori, giacché i raggi estremi concorrono gli uni verso gli altri, e ciò restringe le ombre. Maggiori dei corpi sono le ombre quando le sorgenti sono minori, giacché in questo caso accade che i raggi estremi si diffondono, rendendo così maggiore la parte adombrata.

Ma di ombre ne parla già, nel V/IV sec. a.C., Platone che, per quanto ne sappiamo, fu il primo a sottolineare l'aspetto dimensionale delle ombre, descrivendo il mito della caverna, riportato nella Repubblica.

Il mito rivela l'esistenza di una popolazione confinata in una caverna con il viso sempre rivolto verso la parete, in modo da non verde altro che le ombre proiettate su di essa.

Possono ricavare informazioni su oggetti di ogni tipo solo analizzando la loro ombra.

L'uomo è sempre stato affascinato dalla posizione delle ombre, come possiamo notare esaminando disposizione e orientamento dei templi. Spesso venivano costruiti in modo da tenere conto della posizione del Sole e dell'ombra che avrebbe proiettato in certi momenti cruciali dell'anno.

Molte di queste strutture funzionavano di fatto come rudimentali osservatori: permettevano di identificare in modo preciso alcuni giorni particolari, come i solstizi o gli equinozi, proprio grazie alle ombre proiettate sul terreno.

Anche una meridiana in fondo non è altro che uno strumento che trasforma il trascorrere del tempo nel movimento di un'ombra su un piano.

Un'ombra è una immagine proiettata su una superficie, generalmente piana, da un oggetto interposto fra questa superficie e una sorgente di luce.

Ci sono due modi di considerare le immagini-ombra, modi riferiti alla tipologia della sorgente luminosa: il caso in cui tale sorgente è il Sole e allora si considerano i raggi paralleli tra loro (Eratostene docet) e il caso in cui la sorgente è una luce puntiforme (prospettiva e proiezioni).

Il Sole come sorgente (Affinità)

E' possibile matematizzare la procedura di formazione delle ombre solari attraverso l'uso delle affinità, una trasformazione geometrica che conserva: a) l’allineamento dei punti, b) il parallellismo delle rette.

Perde invece l’ampiezza degli angoli e non si conserva la distanza dei punti.

La relazione tra un oggetto e la sua ombra è un esempio di affinità.

Nel piano cartesiano le affinità si possono tradurre in equazioni lineari.

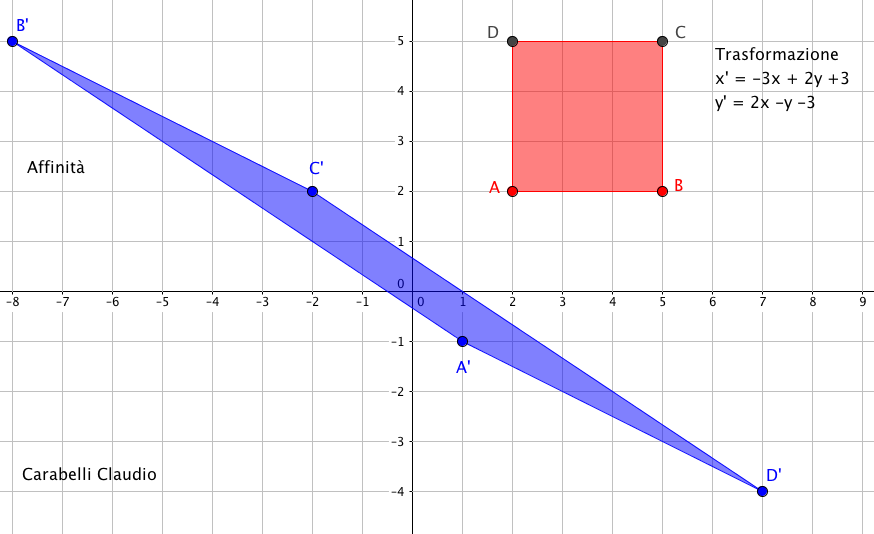
Ad esempio data la trasformazione (vedi figura sottostante):

X' = -3x + 2y + 3

Y' = 2x - y -3

il quadrato A (2;2), B (5;2), C (5;5), D(2;5) si trasforma nel parallelogramma A' (1;-1), B' (-8;+5), C' (-2;2), D' (7;-4).

Nella trasformazione la condizione di parallelismo fra elementi geometrici paralleli viene mantenuta (invariante), ma non quella di perpendicolarità, come si può facilmente verificare nella formazione delle ombre solari.

Il punto luce come sorgente (Proiettività)

Se invece le ombre di un oggetto sono generate da un punto luce (torcia, lampadina),

allora si deve ricorrere ad un nuovo modello matematico. In questo caso il quadrato ABCD è trasformato nel quadrilatero A’B’C’D’.

Questa trasformazione si chiama proiettività.

In essa si conserva l’allineamento dei punti, ma si perde il parallelismo delle rette.

Non si conserva l’ampiezza degli angoli né la distanza dei punti.

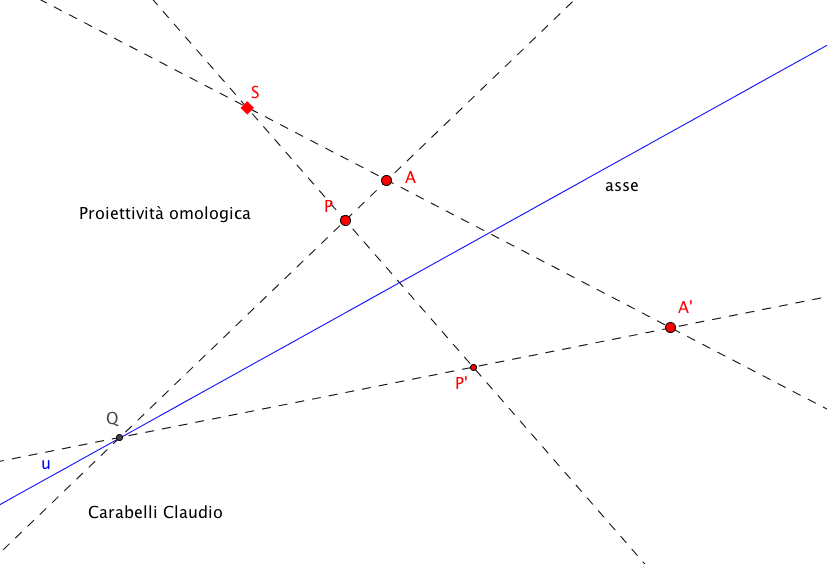
Fissati nel piano una retta u, detta asse della proiettività omologica, un punto S non appartenente ad u, detto centro di proiezione, un punto A e il suo corrispondente A', allineati con S, a ogni punto P del piano, diverso da S, si fa corrispondere il punto P', così ottenuto:

• si traccia la retta AP e si determina il punto Q in cui tale retta interseca l’asse u;

• si traccia la retta SP;

• si traccia la retta QA′ che interseca la retta SP nel punto P′, corrispondente di P nella proiettività omologica.

Nel caso di sinistra (raggi provenienti dall'infinito, considerati paralleli) le colonne parallele generano ombre che si mantengono parallele fra loro; nel caso di destra la condizione di parallelismo, per gli elementi verticali, non è più invariante.

Ed è proprio a questo secondo caso a cui faremo riferimento.

Questo scenario ci consente di usare le ombre per ottenere immagini di strutture complicate nello spazio tridimensionale e, per estensione, anche in spazi a più dimensioni.

Quindi quando guardiamo un cubo (prospettiva con un punto di fuga, con due punti di fuga, con tre punti di fuga), i suoi elementi più vicini hanno immagini più grandi, quelli più lontani immagini più piccole.

Memorizziamo quanto precedentemente scritto e tentiamo ora di interpretare strutture tridimensionali a partire dalla loro ombra proiettata su superficie piana.

Quale poliedro (regolare) riusciamo a ricostruire osservando la sua ombra e siamo in grado di identificarlo?

Possiamo fare alcune considerazioni: le facce del poliedro sono pentagoni, vi sono 5 pentagoni "inferiori" e 5 "superiori"; a questi si devono aggiungere 2 basi anch'esse pentagonali; ad ogni vertice del poliedro convergono 3 facce; quindi il poliedro è caratterizzato da 12 facce, 20 vertici e 30 spigoli.

Non può che trattarsi di un dodecaedro, l'elemento che Platone riconosce come rappresentativo della quintessenza (luce) dell'Universo!

Torniamo al titolo dell'articolo e concludiamolo immaginando di essere moderni baroni di Munchausen e di cavalcare un raggio di luce.

Una delle applicazioni più emozionanti della luce è quella del teatro nero: spettacoli di danza illuminati con luce ultravioletta in cui sono visibili solo quelle porzioni dei corpi ricoperte da costumi fluorescenti.

Colpito da momentanea eclissi, il mio passato non proiettava più davanti a me quell'ombra di sé stesso che chiamiamo futuro; ponendo lo scopo della mia vita non più nella realizzazione dei sogni del passato, ma nella felicità dell'attimo presente, non vedevo più in là di questo.

La Recherche, Marcel Proust

Mio caro Marcel, ti mancava proprio la matematica...